Year 7-12 Curriculum Acceleration & SACE/IB Programs (Adelaide)

Year 7-12 Curriculum Acceleration & SACE/IB Programs (Adelaide)
- 2024 Y9-12 Maths & Science Headstart (Holiday) Programs
- Class Timetable (Weekends)
- AMC & Mathematical Reasoning
- Science Programs
- Mathematical Methods Acceleration
- Chemistry Acceleration
- Biology Acceleration
- English / English Literary Studies
- Specialist Maths Acceleration
- Physics Acceleration
- Research Project
- 2023 Term Break Holiday Programs
2024 Years 9 and 10
Maths & Science Enrichment (Holiday) Program
(08/01/2024-20/01/2024)
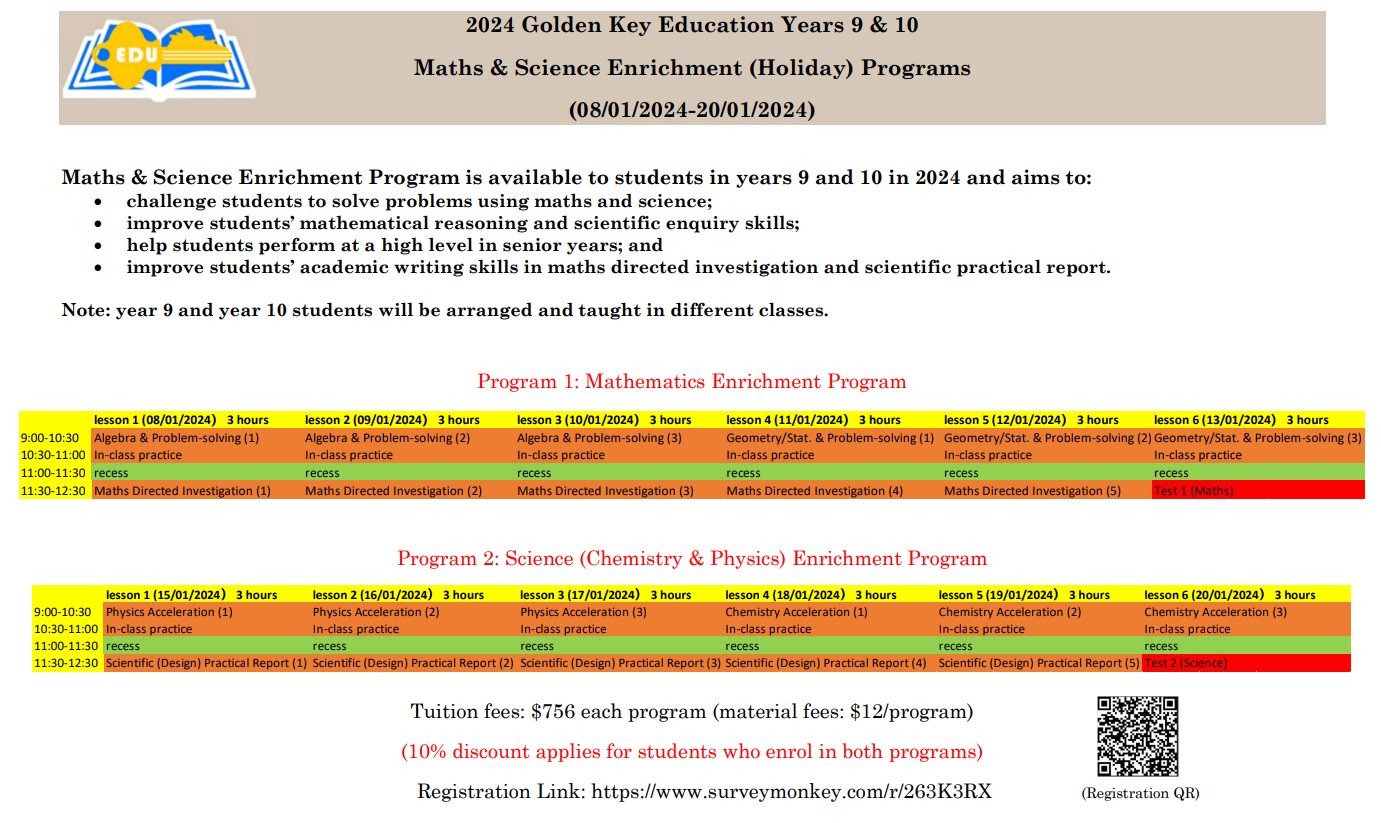
>>Click Here to Registration<< https://www.surveymonkey.com/r/263K3RX
2024 Year 11 SACE Headstart Program
for
Specialist Maths, Maths Methods, Physics, Chemistry
(08/01/2024-19/01/2024)
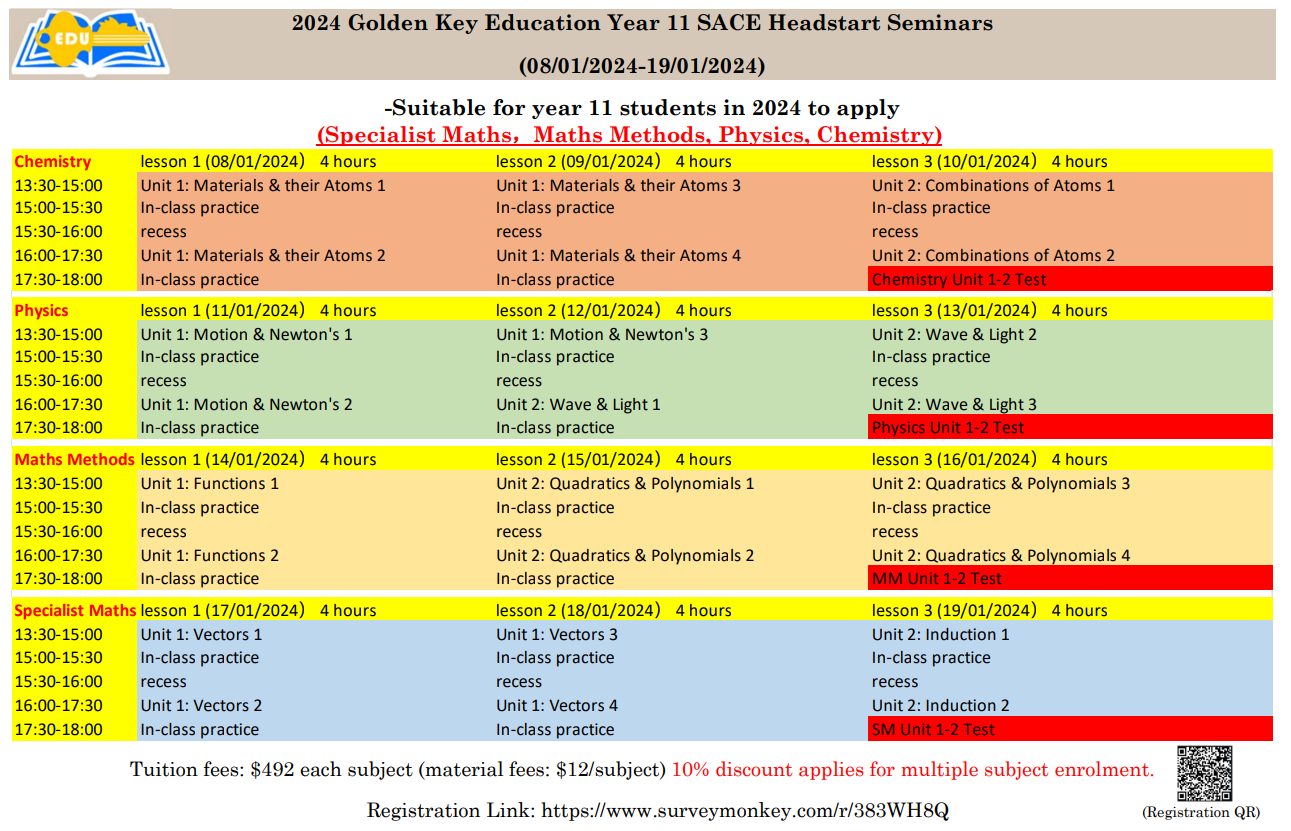
>>Click Here to Registration<< https://www.surveymonkey.com/r/383WH8Q
2024 Year 12 SACE Headstart Program
for
Specialist Maths, Maths Methods, Physics, Chemistry
(16/12/2023-21/12/2023 & 08/01/2024-22/01/2024)
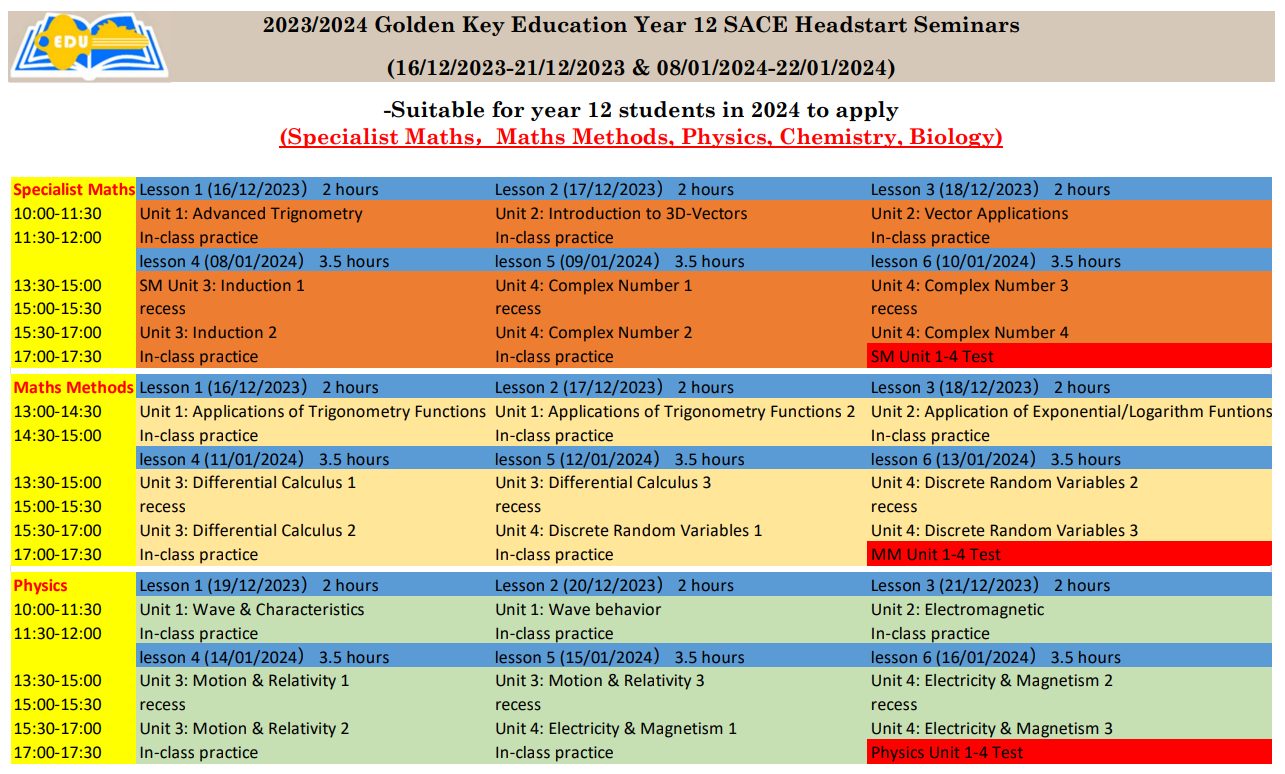
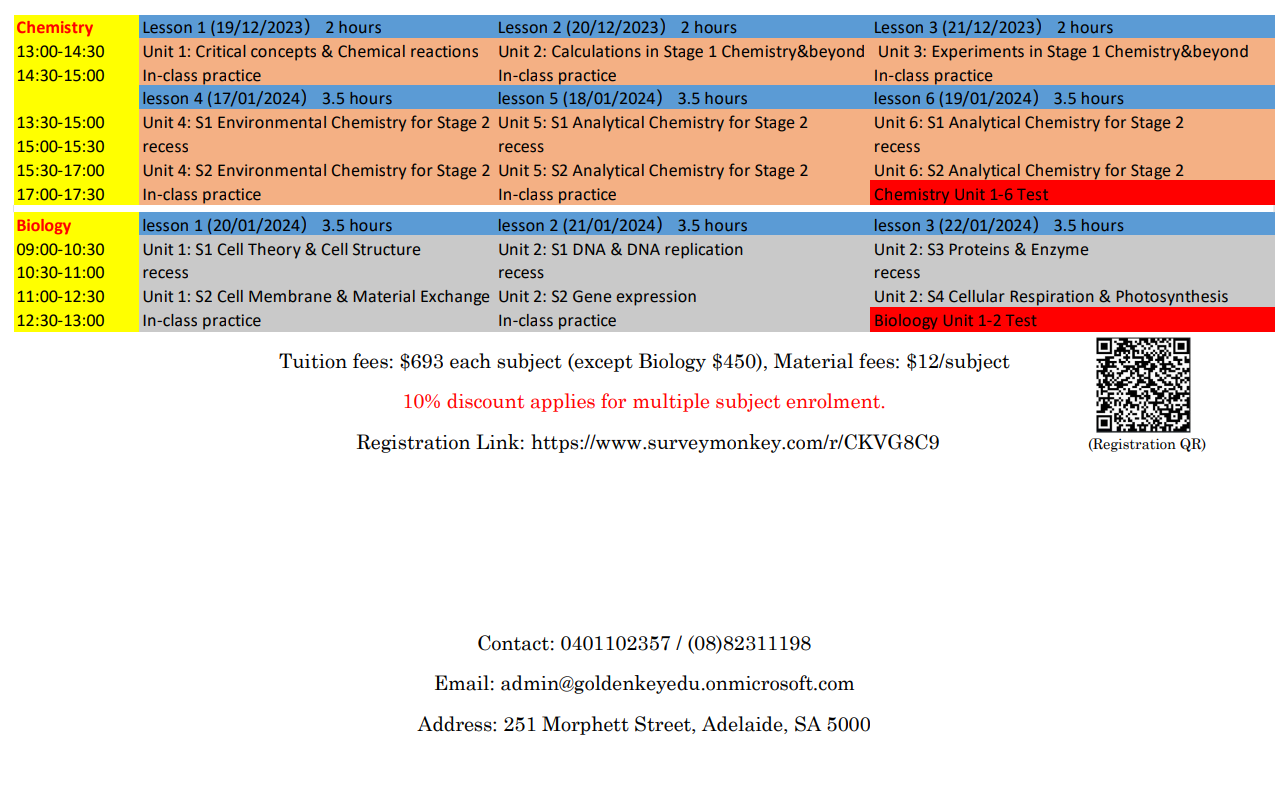
>>Click Here to Registration<<
https://www.surveymonkey.com/r/CKVG8C9
The timetable on Saturdays (Part)
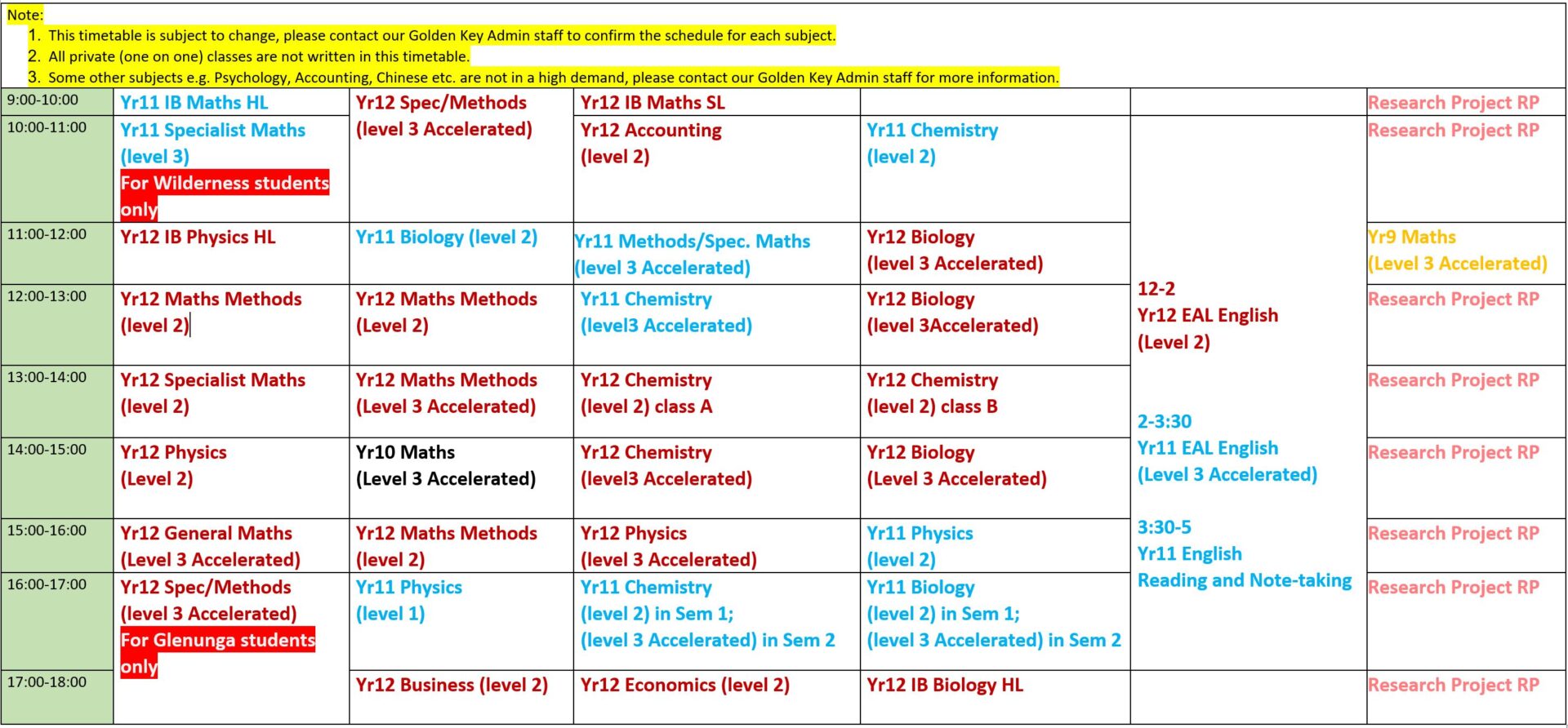
The timetable on Sundays (Part)
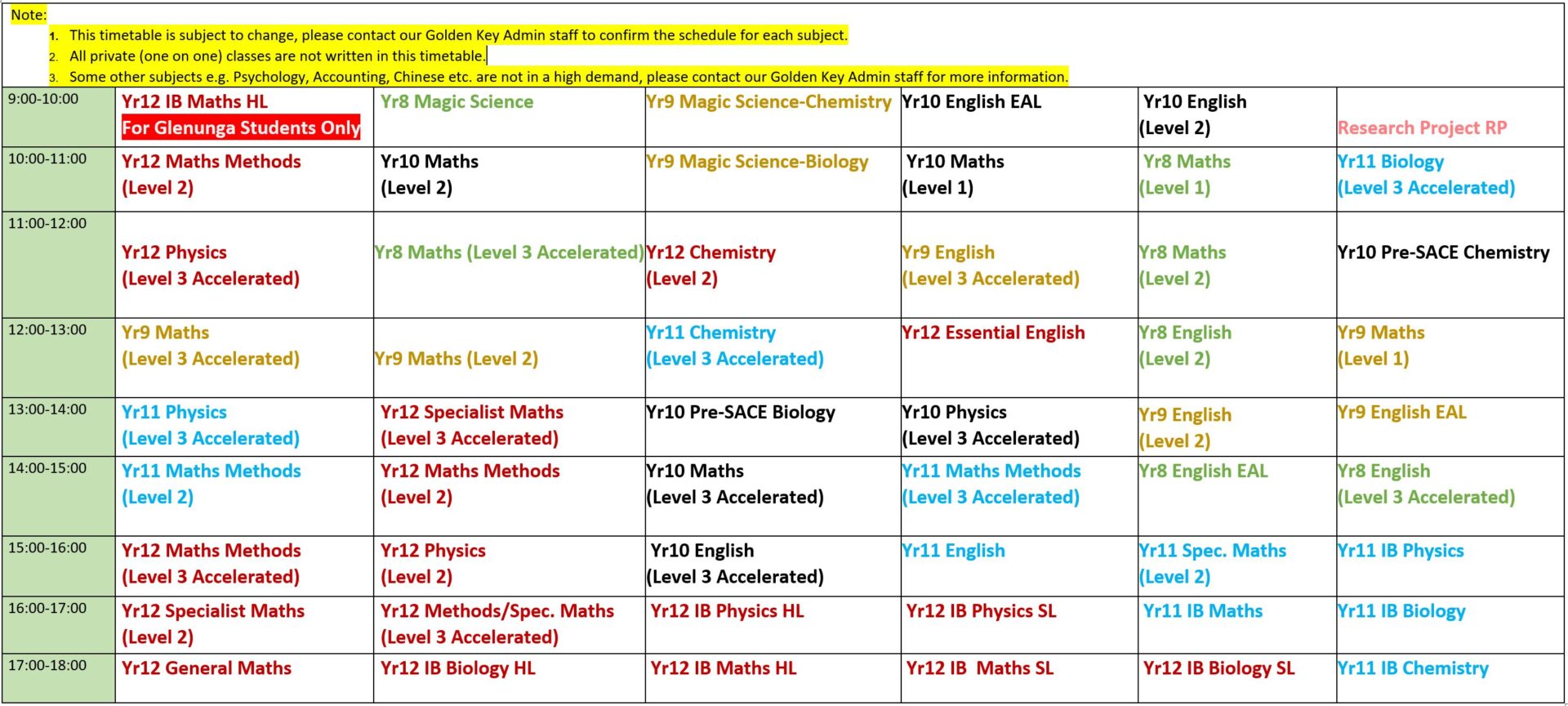
Our Programs (Core)
Maths Olympiads / AMC (Sample Questions)
Year 7-9 Science Programs
The Magic Science series is a course based on scientific experiments and activities relevant to everyday life, with a focus on the study of chemistry, physics, biology, astronomy and geology as well as their related academic vocabulary and scientific theories.
Under the guidance of our experienced tutors, students are encouraged to design and participate in scientific experiments and discover interesting scientific phenomena and solve problems to fully stimulate the students' interest in scientific exploration and learning. Additionally, students are also taught to summarize experiment results in an accurate and logical manner.
Magic Science is a science exploration class for students from grades 7-9. The course incorporates the scientific academic vocabulary required by ACARA (Australian Curriculum, Assessment and Reporting Authority) for grades 8-10 and integrates the vocabulary and scientific concepts into more than 100 carefully selected science activities that are relevant to everyday life.
To better help students in grades 8-9 to lay a strong foundation for scientific theory as fast as possible, Golden Key Education has also organized a team of science teachers specifically for this course. The team has developed and compiled the curriculum from a combination of science competitions (Aus. Science Olympiads) and 11th and 12th grade science learning content. Each team member is not only registered but is also a professional teacher with backgrounds in 11th to 12th grade physics, chemistry and biology. Refer to 'Sample Booklets' for more details.
Course Description
Overview of the Accelerated Program for Mathematical Methods
Click for details
Overview of the Accelerated Program for Chemistry
The first year of the Program makes sure that learners will have: (1) flawless understanding of atomic structures and properties of common elements and compounds; (2) an extensive knowledge of common chemical reactions and how they play in real life; (3) excellent literacy skills in using academic language to describe chemical changes and reflect on experiment results.
The second year of the Program makes sure that learners, apart from a successful completion of SACE Stage 1 Chemistry curriculum, will achieve equivalent to SACE Stage 2 level on the following topics: Elemental Chemistry, Stoichiometry, Organic Chemistry and Biochemistry. By the end of the Accelerated Program, students will be able to commence revision on the above topics and half exams to further prepare for SACE Stage 2 assessments.
Through a variety of learning activities, including hands-on experiments, thinking challenges, productive discussions and prompt assessment tasks and so on, students are expected to become successful science learners, confident problem solvers and high-ATAR achievers.
Click for details
Overview of the Accelerated Program for Biology
To do such, students will be briefly introduced to some view of philosophy and the distinctive features of sciences, recognize falsifiability as a central principle in theory progression. Students will also be led through classical and modern cases of theoretical development. So that students will exercise their critical thinking and understand scientific bases and processes. Through journal club sessions, students will gain a deep insight into modern biological research, which includes agricultural, medical to ecological aspects. Knowledge delivery will be logically arranged as a scientific cycle. The key aspects of sciences will be practiced over the six main topics of biology, which covers all year 11 to 12 contents (the origin of life, molecular biology, cytology, physiology, immunology and epidemiology, ecology and evolution).
Click for details
Overview of the Accelerated Program for English / English Literary Studies
English Standard Accelerator is a 21-week subject designed specifically to help Year 11 and 12 students excel in their grades for English Standard. English Standard Accelerator consists of multiple assessment tasks covering all three key topics taught in the official SACE subjects: Responding to Texts, Creating Texts, and the Intertextual Study / Comparative Analysis tasks. English Standard Accelerator contains a full year’s worth of content within only one semester. This helps students stay consistently ahead by practicing English assessment types long before they are due in school.
请点击浏览课程详情
Overview of the Accelerated Program for Specialist Maths
Click for details
Overview of the Accelerated Program for Physics
Click for details
Overview of the Accelerated Program for GOLDEN KEY RESEARCH PROJECT
The Research Project gives students the opportunity to study a topic of their choice in depth, while learning key research and evaluation techniques needed for all other areas of study and life. Research project may seem difficult, but it can be very useful for future study paths and careers, and also very enjoyable. It allows students to:
• Spend time learning about a topic of their choice that they are truly interested in
• Immerse themselves within a community
• Enjoy the flexibility of the subject, as students are able to work to their strengths
• Enjoy completing work that is different to their typical subjects
• Produce their own tangible, original research
• Creating University and career connections, though primary interactions
• Build key skills needed across all subjects in school and university, such as: • Critical source evaluation • English and academic writing skills • Data analysis • Referencing • Time management
STAGES OF THE PROJECT
There are three stages of the Research Project
• Folio: The Folio is the story of how the research was completed and includes the thoughts, ideas, analysis, and changes, through every step of the research. It highlights what was done and why, and how one thing led to another. It is only 10 pages long, so every bit of space counts. A misconception of the Folio is that every source analysis should be included, but instead it should be about showing the development of the research, and specifically the most important sources that ‘shaped’ the research process.
• Outcome: The Outcome is the result of all the hard work in the Folio, and should be presented in a way to enhance the research findings. The format of the Outcome should suit the research topic, and also the strengths of the student. It should have a tailored, target audience, and be very easy to follow and understand the key findings of the research.
• Evaluation: The Evaluation discusses the work completed throughout research project, and the decisions made. This is an opportunity to be critical, and discuss how useful or limited decisions made were, as well as how well the research question was answered. A misconception of the Evaluation is to focus on the challenges experienced, but instead, the focus should be on how well the challenges were responded to, how they were turned into opportunities, and how they shaped the research.
RESEARCH WITH GUIDANCE The Research Project can be confusing and overwhelming, but it is an extremely useful learning process, and can be made simple with some helpful tips and guidance. Student will focus on and be assisted with:
• Critical and academic English writing
• Essential research vocabulary
• Extremely thorough drafting
• Evaluating and finalising a research topic and question
• Planning for and creating primary interactions such as surveys, interviews etc.
• Selecting suitable secondary sources, and access to academic resources and databases
• Evaluating resources for validity, reliability, credibility, bias etc.
• Organising and categorising information and sources in order to make researching and writing the outcome much easier
• Referencing
• Visual design of assignments
Our Research Project Coordinator, Zoe Gomez, is the main tutor guiding our students through the Research Project, and has had great success assisting students in the past. Through her understanding and experience of the research project, she is able to help students achieve their best work. She completed high school with a 99.0 ATAR and an A+ with merit in Research Project and Information Publishing and Processing. She was also asked to speak at the SACE exhibition about her work and experience with the Research Project. She is always available through email to answer any questions students have about their research, no matter how simple or complicated, and is excited to help students achieve their best and enjoy the research project.
2023 Term 2 Holiday Programs (19/07/2023 - 21/07/2023)
Academic Writing for Scientific Practical Reports
To improve learner’s literacy in academic writing through introducing:
1. Structures of scientific reports;
2. Language features of practical reports;
3. Common phrases, expressions and sentence structures appropriate for writing;
4. Approaches to data collection, processing and analysis;
5. Identification and reflection on sources of errors in experiments;
6. Polishing a practical report according to SACE performance standards.
>>Click here to register for Academic Writing for Scientific Practical Reports Program<<


Year 7-12 Achievement Standards
- English/EAL
- Mathematics/Maths Methods/Specialist Maths/General Maths
- General Science/Physics/Chemistry/Biology
- Other SACE Subjects
Year 8 English Achievement Standard
Receptive modes (listening, reading and viewing) By the end of Year 8, students understand how the selection of text structures is influenced by the selection of language mode and how this varies for different purposes and audiences. Students explain how language features, images and vocabulary are used to represent different ideas and issues in texts.Students interpret texts, questioning the reliability of sources of ideas and information. They select evidence from the text to show how events, situations and people can be represented from different viewpoints. They listen for and identify different emphases in texts, using that understanding to elaborate on discussions.
Productive modes (speaking, writing and creating) Students understand how the selection of language features can be used for particular purposes and effects. They explain the effectiveness of language choices they make to influence the audience. Through combining ideas, images and language features from other texts, students show how ideas can be expressed in new ways.
Students create texts for different purposes, selecting language to influence audience response. They make presentations and contribute actively to class and group discussions, using language patterns for effect. When creating and editing texts to create specific effects, they take into account intended purposes and the needs and interests of audiences. They demonstrate understanding of grammar, select vocabulary for effect and use accurate spelling and punctuation.
Year 9 English Achievement Standard
Receptive modes (listening, reading and viewing) By the end of Year 9, students analyse the ways that text structures can be manipulated for effect. They analyse and explain how images, vocabulary choices and language features distinguish the work of individual authors. They evaluate and integrate ideas and information from texts to form their own interpretations. They select evidence from texts to analyse and explain how language choices and conventions are used to influence an audience. They listen for ways texts position an audience.Productive modes (speaking, writing and creating) Students understand how to use a variety of language features to create different levels of meaning. They understand how interpretations can vary by comparing their responses to texts to the responses of others. In creating texts, students demonstrate how manipulating language features and images can create innovative texts.
Students create texts that respond to issues, interpreting and integrating ideas from other texts. They make presentations and contribute actively to class and group discussions, comparing and evaluating responses to ideas and issues. They edit for effect, selecting vocabulary and grammar that contribute to the precision and persuasiveness of texts and using accurate spelling and punctuation.
Year 10 English Achievement Standard
Receptive modes (listening, reading and viewing) By the end of Year 10, students evaluate how text structures can be used in innovative ways by different authors. They explain how the choice of language features, images and vocabulary contributes to the development of individual style.They develop and justify their own interpretations of texts. They evaluate other interpretations, analysing the evidence used to support them. They listen for ways features within texts can be manipulated to achieve particular effects. Productive modes (speaking, writing and creating) Students show how the selection of language features can achieve precision and stylistic effect. They explain different viewpoints, attitudes and perspectives through the development of cohesive and logical arguments. They develop their own style by experimenting with language features, stylistic devices, text structures and images.
Students create a wide range of texts to articulate complex ideas. They make presentations and contribute actively to class and group discussions, building on others' ideas, solving problems, justifying opinions and developing and expanding arguments. They demonstrate understanding of grammar, vary vocabulary choices for impact, and accurately use spelling and punctuation when creating and editing texts.
Year 11 EAL/ESL
Semester 1:Learning Outcomes
By the end of this unit, students:
• communicate ideas and opinions in a range of contexts
• demonstrate literal and inferential comprehension of information, ideas and language used in texts
• understand and apply social and cultural references from different contexts
• plan and create oral, written and multimodal texts appropriate to purpose and audience.
Semester 2:
Learning Outcomes
By the end of this unit, students:
• use communication skills to analyse and compare attitudes and values in texts
• demonstrate literal and inferential comprehension of information, ideas and language used in texts
• understand personal, social and cultural attitudes and perspectives in a range of texts from different contexts
• plan, create and refine oral, written and multimodal texts appropriate to context, purposes and audiences.
Year 8 Achievement Mathematics Standard
By the end of Year 8, students solve everyday problems involving rates, ratios and percentages. They describe index laws and apply them to whole numbers. They describe rational and irrational numbers. Students solve problems involving profit and loss. They make connections between expanding and factorising algebraic expressions. Students solve problems relating to the volume of prisms. They make sense of time duration in real applications. They identify conditions for the congruence of triangles and deduce the properties of quadrilaterals. Students model authentic situations with two-way tables and Venn diagrams. They choose appropriate language to describe events and experiments. They explain issues related to the collection of data and the effect of outliers on means and medians in that data.Students use efficient mental and written strategies to carry out the four operations with integers. They simplify a variety of algebraic expressions. They solve linear equations and graph linear relationships on the Cartesian plane. Students convert between units of measurement for area and volume. They perform calculations to determine perimeter and area of parallelograms, rhombuses and kites. They name the features of circles and calculate the areas and circumferences of circles. Students determine the probabilities of complementary events and calculate the sum of probabilities.
Year 9 Mathematics Achievement Standard
By the end of Year 9, students solve problems involving simple interest. They interpret ratio and scale factors in similar figures. Students explain similarity of triangles. They recognise the connections between similarity and the trigonometric ratios. Students compare techniques for collecting data from primary and secondary sources. They make sense of the position of the mean and median in skewed, symmetric and bi-modal displays to describe and interpret data.Students apply the index laws to numbers and express numbers in scientific notation. They expand binomial expressions. They find the distance between two points on the Cartesian plane and the gradient and midpoint of a line segment. They sketch linear and non-linear relations. Students calculate areas of shapes and the volume and surface area of right prisms and cylinders. They use Pythagoras’ Theorem and trigonometry to find unknown sides of right-angled triangles. Students calculate relative frequencies to estimate probabilities, list outcomes for two-step experiments and assign probabilities for those outcomes. They construct histograms and back-to-back stem-and-leaf plots.
Year 10/10A Mathematics Achievement Standard
By the end of Year 10, students recognise the connection between simple and compound interest. They solve problems involving linear equations and inequalities. They make the connections between algebraic and graphical representations of relations. Students solve surface area and volume problems relating to composite solids. They recognise the relationships between parallel and perpendicular lines. Students apply deductive reasoning to proofs and numerical exercises involving plane shapes. They compare data sets by referring to the shapes of the various data displays. They describe bivariate data where the independent variable is time. Students describe statistical relationships between two continuous variables. They evaluate statistical reports.Students expand binomial expressions and factorise monic quadratic expressions. They find unknown values after substitution into formulas. They perform the four operations with simple algebraic fractions. Students solve simple quadratic equations and pairs of simultaneous equations. They use triangle and angle properties to prove congruence and similarity. Students use trigonometry to calculate unknown angles in right-angled triangles. Students list outcomes for multi-step chance experiments and assign probabilities for these experiments. They calculate quartiles and inter-quartile ranges.
Year 11 General Mathematics
Semester 1:Description
This unit has three topics: ‘Consumer arithmetic’, ‘Algebra and matrices’, and ‘Shape and measurement’.
‘Consumer arithmetic’ reviews the concepts of rate and percentage change in the context of earning and managing money, and provides a fertile ground for the use of spreadsheets.
‘Algebra and matrices’ continues the F-10 study of algebra and introduces the new topic of matrices.
‘Shape and measurement’ builds on and extends the knowledge and skills students developed in the F-10 curriculum with the concept of similarity and associated calculations involving simple and compound geometric shapes. The emphasis in this topic is on applying these skills in a range of practical contexts, including those involving three-dimensional shapes.
Classroom access to the technology necessary to support the computational aspects of the topics in this unit is assumed.
Learning Outcomes
By the end of this semester, students:
• understand the concepts and techniques introduced in consumer arithmetic, algebra and matrices, and shape and measurement
• apply reasoning skills and solve practical problems arising in consumer arithmetic, algebra and matrices, and shape and measurement
• communicate their arguments and strategies, when solving problems, using appropriate mathematical language
• interpret mathematical information, and ascertain the reasonableness of their solutions to problems
• choose and use technology appropriately and efficiently.
Semester 2:
Description
This unit has three topics: ‘Univariate data analysis and the statistical investigation process’, ‘Linear equations and their graphs’; and ‘Applications of trigonometry’.
‘ Univariate data analysis and the statistical investigation process’ develops students’ ability to organise and summarise univariate data in the context of conducting a statistical investigation.
‘Linear equations and their graphs’ uses linear equations and straight-line graphs, as well as linear-piecewise and step graphs, to model and analyse practical situations.
‘Applications of trigonometry’ extends students’ knowledge of trigonometry to solve practical problems involving non-right-angled triangles in both two and three dimensions, including problems involving the use of angles of elevation and depression and bearings in navigation.
Classroom access to the technology necessary to support the graphical, computational and statistical aspects of this unit is assumed.
Learning Outcomes
By the end of this semester, students:
• understand the concepts and techniques in univariate data analysis and the statistical investigation process, linear equations and their graphs, and applications of trigonometry
• apply reasoning skills and solve practical problems in univariate data analysis and the statistical investigation process, linear equations and their graphs, and the applications of trigonometry
• implement the statistical investigation process in contexts requiring the analysis of univariate data
• communicate their arguments and strategies, when solving mathematical and statistical problems, using appropriate mathematical or statistical language
• interpret mathematical and statistical information, and ascertain the reasonableness of their solutions to problems and their answers to statistical questions
• choose and use technology appropriately and efficiently.
Year 11 Mathematical Methods
Semester 1:Description
This unit begins with a review of the basic algebraic concepts and techniques required for a successful introduction to the study of calculus. The basic trigonometric functions are then introduced. Simple relationships between variable quantities are reviewed, and these are used to introduce the key concepts of a function and its graph. The study of inferential statistics begins in this unit with a review of the fundamentals of probability and the introduction of the concepts of conditional probability and independence. Access to technology to support the computational aspects of these topics is assumed.
Learning Outcomes By the end of this unit, students:
• understand the concepts and techniques in algebra, functions, graphs, trigonometric functions and probability
• solve problems using algebra, functions, graphs, trigonometric functions and probability
• apply reasoning skills in the context of algebra, functions, graphs, trigonometric functions and probability
• interpret and evaluate mathematical information and ascertain the reasonableness of solutions to problems
• communicate their arguments and strategies when solving problems.
Semester 2:
Unit Description
The algebra section of this unit focuses on exponentials and logarithms. Their graphs are examined and their applications in a wide range of settings are explored. Arithmetic and geometric sequences are introduced and their applications are studied. Rates and average rates of change are introduced, and this is followed by the key concept of the derivative as an ‘instantaneous rate of change’. These concepts are reinforced numerically, by calculating difference quotients both geometrically, as slopes of chords and tangents, and algebraically. Calculus is developed to study the derivatives of polynomial functions, with simple applications of the derivative to curve sketching, calculating slopes and equations of tangents, determining instantaneous velocities and solving optimisation problems. Access to technology to support the computational aspects of these topics is assumed.
Learning Outcomes
By the end of this unit, students:
• understand the concepts and techniques used in algebra, sequences and series, functions, graphs and calculus
• solve problems in algebra, sequences and series, functions, graphs and calculus
• apply reasoning skills in algebra, sequences and series, functions, graphs and calculus
• interpret and evaluate mathematical and statistical information and ascertain the reasonableness of solutions to problems
• communicate arguments and strategies when solving problems.
Year 11 Specialist Mathematics
Semester 1:Description
Unit 1 of Specialist Mathematics contains three topics – ‘Combinatorics’, ‘Vectors in the plane’ and ‘Geometry’ – that complement the content of Mathematical Methods. The proficiency strand, Reasoning, of the F–10 curriculum is continued explicitly in ‘Geometry’ through a discussion of developing mathematical arguments. While these ideas are illustrated through deductive Euclidean geometry in this topic, they recur throughout all of the topics in Specialist Mathematics. ‘Geometry’ also provides the opportunity to summarise and extend students’ studies in Euclidean Geometry. An understanding of this topic is of great benefit in the study of later topics in the course, including vectors and complex numbers.
‘Vectors in the plane’ provides new perspectives for working with two-dimensional space, and serves as an introduction to techniques that will be extended to three-dimensional space in Unit 3.
‘Combinatorics’ provides techniques that are useful in many areas of mathematics including probability and algebra. All these topics develop students’ ability to construct mathematical arguments.
These three topics considerably broaden students’ mathematical experience and therefore begin an awakening to the breadth and utility of the subject. They also enable students to increase their mathematical flexibility and versatility.
Access to technology to support the computational aspects of these topics is assumed.
Learning Outcomes
By the end of this unit, students:
• understand the concepts and techniques in combinatorics, geometry and vectors
• apply reasoning skills and solve problems in combinatorics, geometry and vectors
• communicate their arguments and strategies when solving problems
• construct proofs in a variety of contexts including algebraic and geometric
• interpret mathematical information and ascertain the reasonableness of their solutions to problems.
Semester 2:
Unit Description
Unit 2 of Specialist Mathematics contains three topics – ‘Trigonometry’, ‘Real and complex numbers’ and ‘Matrices’… ‘Trigonometry’ contains techniques that are used in other topics in both this unit and Unit 3. ‘Real and complex numbers’ provides a continuation of students’ study of numbers, and the study of complex numbers is continued in Unit 3. This topic also contains a section on proof by mathematical induction. The study of matrices is undertaken, including applications to linear transformations of the plane.
Access to technology to support the computational aspects of these topics is assumed.
Learning Outcomes
By the end of this unit, students:
• understand the concepts and techniques in trigonometry, real and complex numbers, and matrices
• apply reasoning skills and solve problems in trigonometry, real and complex numbers, and matrices
• communicate their arguments and strategies when solving problems • construct proofs of results
• interpret mathematical information and ascertain the reasonableness of their solutions to problems.
Year 8 Science Achievement Standard
By the end of Year 8, students compare physical and chemical changes and use the particle model to explain and predict the properties and behaviours of substances. They identify different forms of energy and describe how energy transfers and transformations cause change in simple systems. They compare processes of rock formation, including the timescales involved. They analyse the relationship between structure and function at cell, organ and body system levels. Students examine the different science knowledge used in occupations. They explain how evidence has led to an improved understanding of a scientific idea and describe situations in which scientists collaborated to generate solutions to contemporary problems. They reflect on implications of these solutions for different groups in society.Students identify and construct questions and problems that they can investigate scientifically. They consider safety and ethics when planning investigations, including designing field or experimental methods. They identify variables to be changed, measured and controlled. Students construct representations of their data to reveal and analyse patterns and trends, and use these when justifying their conclusions. They explain how modifications to methods could improve the quality of their data and apply their own scientific knowledge and investigation findings to evaluate claims made by others. They use appropriate language and representations to communicate science ideas, methods and findings in a range of text types.
Year 9 Science Achievement Standard
By the end of Year 9, students explain chemical processes and natural radioactivity in terms of atoms and energy transfers and describe examples of important chemical reactions. They describe models of energy transfer and apply these to explain phenomena. They explain global features and events in terms of geological processes and timescales. They analyse how biological systems function and respond to external changes with reference to interdependencies, energy transfers and flows of matter. They describe social and technological factors that have influenced scientific developments and predict how future applications of science and technology may affect people’s lives.
Students design questions that can be investigated using a range of inquiry skills. They design methods that include the control and accurate measurement of variables and systematic collection of data and describe how they considered ethics and safety. They analyse trends in data, identify relationships between variables and reveal inconsistencies in results. They analyse their methods and the quality of their data, and explain specific actions to improve the quality of their evidence. They evaluate others’ methods and explanations from a scientific perspective and use appropriate language and representations when communicating their findings and ideas to specific audiences.
Year 10 Science Achievement Standard
By the end of Year 10, students analyse how the periodic table organises elements and use it to make predictions about the properties of elements. They explain how chemical reactions are used to produce particular products and how different factors influence the rate of reactions. They explain the concept of energy conservation and represent energy transfer and transformation within systems. They apply relationships between force, mass and acceleration to predict changes in the motion of objects. Students describe and analyse interactions and cycles within and between Earth’s spheres. They evaluate the evidence for scientific theories that explain the origin of the universe and the diversity of life on Earth. They explain the processes that underpin heredity and evolution. Students analyse how the models and theories they use have developed over time and discuss the factors that prompted their review.
Students develop questions and hypotheses and independently design and improve appropriate methods of investigation, including field work and laboratory experimentation. They explain how they have considered reliability, safety, fairness and ethical actions in their methods and identify where digital technologies can be used to enhance the quality of data. When analysing data, selecting evidence and developing and justifying conclusions, they identify alternative explanations for findings and explain any sources of uncertainty. Students evaluate the validity and reliability of claims made in secondary sources with reference to currently held scientific views, the quality of the methodology and the evidence cited. They construct evidence-based arguments and select appropriate representations and text types to communicate science ideas for specific purposes.
Year 11 Physics
Learning Outcomes
Semester 1:
By the end of this unit, students:
• understand how the kinetic particle model and thermodynamics concepts describe and explain heating processes
• understand how the nuclear model of the atom explains radioactivity, fission, fusion and the properties of radioactive nuclides
• understand how charge is involved in the transfer and transformation of energy in electrical circuits
• understand how scientific models and theories have developed and are applied to improve existing, and develop new, technologies
• use science inquiry skills to design, conduct and analyse safe and effective investigations into heating processes, nuclear physics and electrical circuits, and to communicate methods and findings
• use algebraic and graphical representations to calculate, analyse and predict measurable quantities associated with heating processes, nuclear reactions and electrical circuits
• evaluate, with reference to empirical evidence, claims about heating processes, nuclear reactions and electrical technologies
• communicate physics understanding using qualitative and quantitative representations in appropriate modes and genres.
Semester 2:
By the end of this unit, students:
• understand how the kinetic particle model and thermodynamics concepts describe and explain heating processes
• understand how the nuclear model of the atom explains radioactivity, fission, fusion and the properties of radioactive nuclides
• understand how charge is involved in the transfer and transformation of energy in electrical circuits
• understand how scientific models and theories have developed and are applied to improve existing, and develop new, technologies
• use science inquiry skills to design, conduct and analyse safe and effective investigations into heating processes, nuclear physics and electrical circuits, and to communicate methods and findings
• use algebraic and graphical representations to calculate, analyse and predict measurable quantities associated with heating processes, nuclear reactions and electrical circuits
• evaluate, with reference to empirical evidence, claims about heating processes, nuclear reactions and electrical technologies
• communicate physics understanding using qualitative and quantitative representations in appropriate modes and genres.
Year 11 Chemistry
Semester 1:
Learning Outcomes
By the end of this unit, students:
• understand how the atomic model and models of bonding explain the structure and properties of elements and compounds
• understand the concept of enthalpy, and apply this to qualitatively and quantitatively describe and explain energy changes in chemical reactions
• understand how models and theories have developed based on evidence from a range of sources, and the uses and limitations of chemical knowledge in a range of contexts
• use science inquiry skills to design, conduct, evaluate and communicate investigations into the properties of elements, compounds and mixtures and the energy changes involved in chemical reactions
• evaluate, with reference to empirical evidence, claims about chemical properties, structures and reactions
• communicate, predict and explain chemical phenomena using qualitative and quantitative representations in appropriate modes and genres.
Semester 2:
Learning Outcomes
By the end of this unit, students:
• understand how models of the shape and structure of molecules and intermolecular forces can be used to explain the properties of substances, including the solubility of substances in water
• understand how kinetic theory can be used to explain the behaviour of gaseous systems, and how collision theory can be used to explain and predict the effect of varying conditions on the rate of reaction
• understand how models and theories have developed based on evidence from multiple disciplines, and the uses and limitations of chemical knowledge in a range of contexts
• use science inquiry skills to design, conduct, evaluate and communicate investigations into the properties and behaviour of gases, water, aqueous solutions and acids and the factors that affect the rate of chemical reactions
• evaluate, with reference to empirical evidence, claims about chemical properties, structures and reactions
• communicate, predict and explain chemical phenomena using qualitative and quantitative representations in appropriate modes and genres.
Year 11 Biology
Semester 1:
Learning Outcomes
By the end of this unit, students:
• understand how classification helps to organise, analyse and communicate data about biodiversity
• understand that ecosystem diversity and dynamics can be described and compared with reference to biotic and abiotic components and their interactions
• understand how theories and models have developed based on evidence from multiple disciplines; and the uses and limitations of biological knowledge in a range of contexts
• use science inquiry skills to design, conduct, evaluate and communicate investigations into biodiversity and flows of matter and energy in a range of ecosystems
• evaluate, with reference to empirical evidence, claims about relationships between and within species, diversity of and within ecosystems, and energy and matter flows
• communicate biological understanding using qualitative and quantitative representations in appropriate modes and genres.
Semester 2:
Learning Outcomes
By the end of this unit, students:
• understand that the structure and function of cells and their components are related to the need to exchange matter and energy with their immediate environment
• understand that multicellular organisms consist of multiple interdependent and hierarchically-organised systems that enable exchange of matter and energy with their immediate environment
• understand how theories and models have developed based on evidence from multiple disciplines; and the uses and limitations of biological knowledge in a range of contexts
• use science inquiry skills to design, conduct, evaluate and communicate investigations into the structure and function of cells and multicellular organisms
• evaluate, with reference to empirical evidence, claims about cellular processes and the structure and function of multicellular organisms
• communicate biological understanding using qualitative and quantitative representations in appropriate modes and genres.
coming soon





